Table Of Contents
USING NITINOL WIRE
Nitinol wire is not easy to use. When it’s all boiled down, there are a number of restrictions that make it awkward to use. The main problem is the current required to activate the product.
For the fine wire, the current cannot be higher than 30mA, for the thicker wire, the current must be greater than 2 amps.
Achieving the exact current is not easy and the voltage you must apply depends on two things:
- The gauge of the wire,
- The length of the wire.
There are two extra factors that need to be taken into account:
- The stability of the supply voltage (the voltage of the battery may fall as it gets older)
- The voltage drop across the activating device (transistor, FET relay etc).
The standard circuit for activating the wire is shown below:
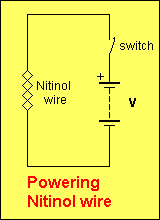
Determining the voltage for a particular length of wire or the most suitable length of wire for a particular voltage, can be obtained from the following calculator:
This calculator takes into account the MAXIMUM current that should be passed though the wire for long life. The table works in INCHES. To convert cm to inches, use the conversion table below.
<!-- TODO FIXME: table with input -->
<!-- FIRST TABLE !---> var A = 0; var B = 0; function clearBoxes1(form) { form.A.value = ""; form.B.value = ""; form.A.focus(); } function showresults1(form) {form.A.value = A; form.B.value = B; } function solve1(form) {var i = 2; if(!form.A.value) A = 0; else A = eval(form.A.value); if(A == 0) i--; if(!form.B.value) B = 0; else B = eval(form.B.value); if(B == 0) i--; if(i == 0) return; if(A != 0) {{B = 0.05 * A * 12; } showresults1(form); form.A.focus(); return; } if(B != 0) { A = B / (12 * 0.05); } showresults1(form); form.B.focus(); return;} <!-- SECOND TABLE !---> var C = 0; var D = 0; function clearBoxes2(form) { form.C.value = ""; form.D.value = ""; form.C.focus(); } function showresults2(form) {form.C.value = C; form.D.value = D; } function solve2(form) {var i = 2; if(!form.C.value) C = 0; else C = eval(form.C.value); if(C == 0) i--; if(!form.D.value) D = 0; else D = eval(form.D.value); if(D == 0) i--; if(i == 0) return; if(C != 0) {{D = 0.18 * C * 3; } showresults2(form); form.C.focus(); return; } if(D != 0) { C = D / (3 * 0.18); } showresults2(form); form.D.focus(); return;} <!-- THIRD TABLE !---> var E = 0; var F = 0; function clearBoxes3(form) { form.E.value = ""; form.F.value = ""; form.E.focus(); } function showresults3(form) {form.E.value = E; form.F.value = F; } function solve3(form) {var i = 2; if(!form.E.value) E = 0; else E = eval(form.E.value); if(E == 0) i--; if(!form.F.value) F = 0; else F = eval(form.F.value); if(F == 0) i--; if(i == 0) return; if(E != 0) {{F = 0.29 * E * 1.9; } showresults3(form); form.E.focus(); return; } if(F != 0) { E = F / (1.9 * 0.29); } showresults3(form); form.F.focus(); return;} <!-- fourth TABLE !---> var G = 0; var H = 0; function clearBoxes4(form) { form.G.value = ""; form.H.value = ""; form.G.focus(); } function showresults4(form) {form.G.value = G; form.H.value = H; } function solve4(form) {var i = 2; if(!form.G.value) G = 0; else G = eval(form.G.value); if(G == 0) i--; if(!form.H.value) H = 0; else H = eval(form.H.value); if(H == 0) i--; if(i == 0) return; if(G != 0) {{H = 0.4 * G * 1.3; } showresults4(form); form.G.focus(); return; } if(H != 0) { G = H / (1.3 * 0.4); } showresults4(form); form.H.focus(); return;} <!-- fifth TABLE !---> var I = 0; var J = 0; function clearBoxes5(form) { form.I.value = ""; form.J.value = ""; form.I.focus(); } function showresults5(form) {form.I.value = I; form.J.value = J; } function solve5(form) {var i = 2; if(!form.I.value) I = 0; else I = eval(form.I.value); if(I == 0) i--; if(!form.J.value) J = 0; else J = eval(form.J.value); if(J == 0) i--; if(i == 0) return; if(I != 0) {{J = 0.61 * I * 0.8; } showresults5(form); form.I.focus(); return; } if(J != 0) { I = J / (0.8 * 0.61); } showresults5(form); form.J.focus(); return;} <!-- SIXTH TABLE !---> var K = 0; var L = 0; function clearBoxes6(form) { form.K.value = ""; form.L.value = ""; form.K.focus(); } function showresults6(form) {form.K.value = K; form.L.value = L; } function solve6(form) {var i = 2; if(!form.K.value) K = 0; else K = eval(form.K.value); if(K == 0) i--; if(!form.L.value) L = 0; else L = eval(form.L.value); if(L == 0) i--; if(i == 0) return; if(K != 0) {{L = 1 * K * 0.5; } showresults6(form); form.K.focus(); return; } if(L != 0) { K = L / 0.5; } showresults6(form); form.L.focus(); return;} <!-- SEVENTH TABLE !---> var M = 0; var N = 0; function clearBoxes7(form) { form.M.value = ""; form.N.value = ""; form.M.focus(); } function showresults7(form) {form.M.value = M; form.N.value = N; } function solve7(form) {var i = 2; if(!form.M.value) M = 0; else M = eval(form.M.value); if(M == 0) i--; if(!form.N.value) N = 0; else N = eval(form.N.value); if(N == 0) i--; if(i == 0) return; if(M != 0) {{N = 1.75 * M * 0.33; } showresults7(form); form.M.focus(); return; } if(N != 0) { M = N / (0.33 * 1.75); } showresults7(form); form.N.focus(); return;} <!-- EIGHTH TABLE !---> var P = 0; var Q = 0; function clearBoxes8(form) { form.P.value = ""; form.Q.value = ""; form.P.focus(); } function showresults8(form) {form.P.value = P; form.Q.value = Q; } function solve8(form) {var i = 2; if(!form.P.value) P = 0; else P = eval(form.P.value); if(P == 0) i--; if(!form.Q.value) Q = 0; else Q = eval(form.Q.value); if(Q == 0) i--; if(i == 0) return; if(P != 0) {{Q = 2.75 * P * 0.2; } showresults8(form); form.P.focus(); return; } if(Q != 0) { P = Q / (0.2 * 2.75); } showresults8(form); form.Q.focus(); return;} <!-- CONVERSION TABLE !---> var R = 0; var S = 0; function clearBoxes9(form) { form.R.value = ""; form.S.value = ""; form.R.focus(); } function showresults9(form) {form.R.value = R; form.S.value = S; } function solve9(form) {var i = 2; if(!form.R.value) R = 0; else R = eval(form.R.value); if(R == 0) i--; if(!form.S.value) S = 0; else S = eval(form.S.value); if(S == 0) i--; if(i == 0) return; if(R != 0) {{S = 2.54 * R; } showresults9(form); form.R.focus(); return; } if(S != 0) { R = S / 2.54; } showresults9(form); form.S.focus(); return;}
0.002” wire
length (in) V =
0.004” wire
length (in) V =
0.005” wire
length (in) V =
0.006” wire
length (in) V =
0.008” wire
length (in) V =
0.010” wire
length (in) V =
0.012” wire
length (in) V =
0.015” wire
length (in) V =
Conversion Table: Convert inches to cm or cm to inches:
length (in) = cm
CONSTANT CURRENT
To prevent Nitinol wire being damaged by excessive current, a constant current circuit can be used to power the wire.
This is a very clever idea as the length of the wire is not important and you can concentrate on:
- The amount of movement you require for the application (the length of the wire), and
- The number of cycles of movement per minute.
The circuit below uses an LM 317 in a constant-current arrangement and the value of resistor R is selected according to the gauge of wire used.
A 7805 can be used in a similar arrangement but the value of R must be changed as the 7805 detects 5v between the “adj” and “out” terminals while the LM317 detects a voltage of 1.2v between these terminals. (The 7805 has a different pinout).
<!-- // TODO FIXME: create cards? -->
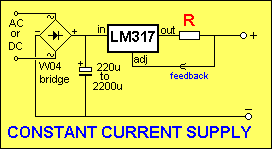
| NITINOL Wire Gauge: | Value of R for circuit above: |
|---|---|
| 0.002 | 24R |
| 0.004 | 6R6 |
| 0.006 | 3R |
| 0.008 | 1R9 |
| 0.010 | 1R2 |
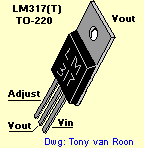
LM 317 is the common name for a 3-terminal adjustable regulator. It comes in three packages:
<!-- // TODO FIXME: create cards? -->
| LM317L | LM317T | LM317K |
|---|---|---|
| Vout 1.2 to 37v | Vout 1.2 to 37v | Vout 1.2 to 37v |
| 10mA to 100mA | 10mA to 1.5A | 10mA to 2.2A |
TO-92

TO-220

TO-3
The T0-3 package must be isolated from earth.
DUTY CYCLE
The LM 317T is rated at 1.5 amp and this means the output voltage will be smooth and steady for a current up to 1.5 amp (smooth voltage is not needed for Nitinol wire).
You will notice from the table on Page 1, the activation time for the wire is 1 second and the off time is from 1sec to 13 seconds, depending on the gauge of the wire. This gives the duty cycle a maximum of 50%, down to less than 10%. This duty cycle also applies to the regulator supplying the current so that any heat produced by the regulator will have time to dissipate into the air via the heat sink when the circuit is not activated. In most cases the regulator will not get very hot and not need a heatsink.
REGULATOR REQUIREMENTS
If you are supplying the circuit from a DC supply, the input voltage to the regulator needs to be 6.1v higher than the voltage required by the Nitinol wire. You can find out the voltage needed by the wire by using the calculator above.
The 6v1 additional voltage is made up of 1.4v drop across the bridge (not needed if supplying DC to the circuit), 3.5v across the regulator (to prevent it “dropping out”) and 1.2v across R. If you are supplying the circuit with AC, the value of AC needs to be determined from the following:
An AC transformer is rated at an output voltage at FULL LOAD. A 12v AC transformer, for example will produce 15v to 17v AC on no-load and drop to 12-14v AC on full load. When rectified, this will produce about 16v DC after the bridge. In other words, this type of transformer will be suitable for a length of Nitinol wire requiring up to a 12v supply.
You can use the 12v AC transformer (or a 12v DC supply) for any length of wire requiring up to 12v.
This is where you really have to know your electrics! You can use any length of any gauge wire that requires up to 12v and/or up to 1.5 amp. The LM 317T does all the adjusting for you.
Providing you fit the correct value resistor for R (according the the current requirement of the wire you are using), you cannot damage the Nitinol wire. You can also use almost any power transformer from 12v AC to 18v AC. Again, the LM 317T will adjust the current to the correct value. The only problem with using a power transformer with a voltage rating higher than 12v AC is the additional heat generated by the regulator chip (the LM 317T). However, as we mentioned above, the duty cycle for Nitinol wire is very small and very little heatsinking will be needed.
THINGS TO COME
I don’t want to upset the applecart but there are new developments in the wind using plastic (ceramic) substrates with metallised terminations to produce deflective movement. These items are still in the experimental stage but require very little current. The life-span seems to be almost infinite and the repetition-rate can be in the kHz and higher. All the limitations of Nitinol will be answered!
It seems amazing but you can understand, it’s only a development away, just like the LED, super-bright LED and the glow-panel. New technology is constantly arriving and sweeping away the old.
For an enormous website on the development of this new product, click HERE. Then Electroactive Polymers (EAP). It is also being turned into Piezo motors and a surface wiper, as shown below:


Piezo motor simulation Surface Wiper using EAP technology
Quick Links
Legal Stuff
Social Media


